1. Giới Thiệu

Cấu tạo

Neural network là thuật toán có cách hoạt động và thành phần cấu tạo tương tự như mạng nơ ron sinh học của con người. Hình dưới là mô tả nơ ron sinh học

Nguồn

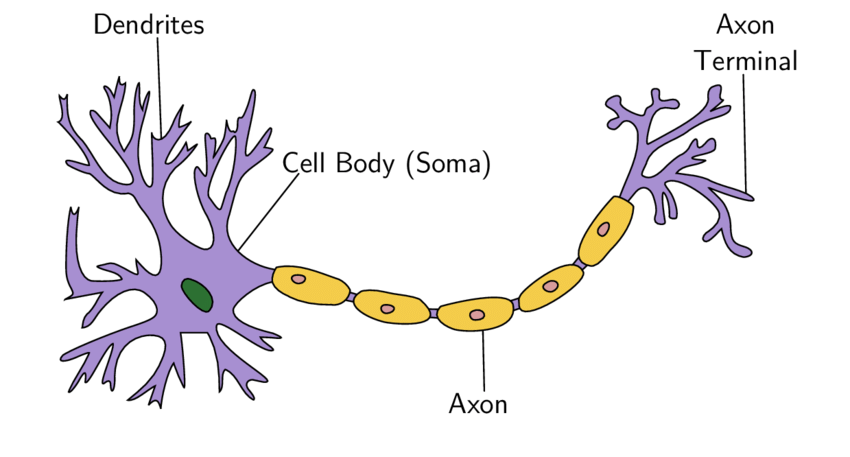
Nơ ron là một tế bào kích thích điện giao tiếp với các tế bào khác, là thành phần chính của mô thần kinh ở hầu hết các loài động vật. Một tế bào thần kinh điển hình bao gồm một cơ thể tế bào (soma),  tiếp nhận tín hiệu đầu vào (input) qua dendrites và một axon xuất các tín hiệu đầu ra (output). Các nơ ron này sẽ nhận tín hiệu ở dendrites, các tín hiệu này sẽ được nơ ron quyết định xem có được đi qua không (ta thấy giống như hàm activate trong nơ ron nhân tạo), nếu được qua thì các tin hiệu này sẽ đến axon và truyền qua các dendrites của các nơ ron khác. Và đây là thành phần cấu tạo của một nơ ron nhân tạo:

Nguồn

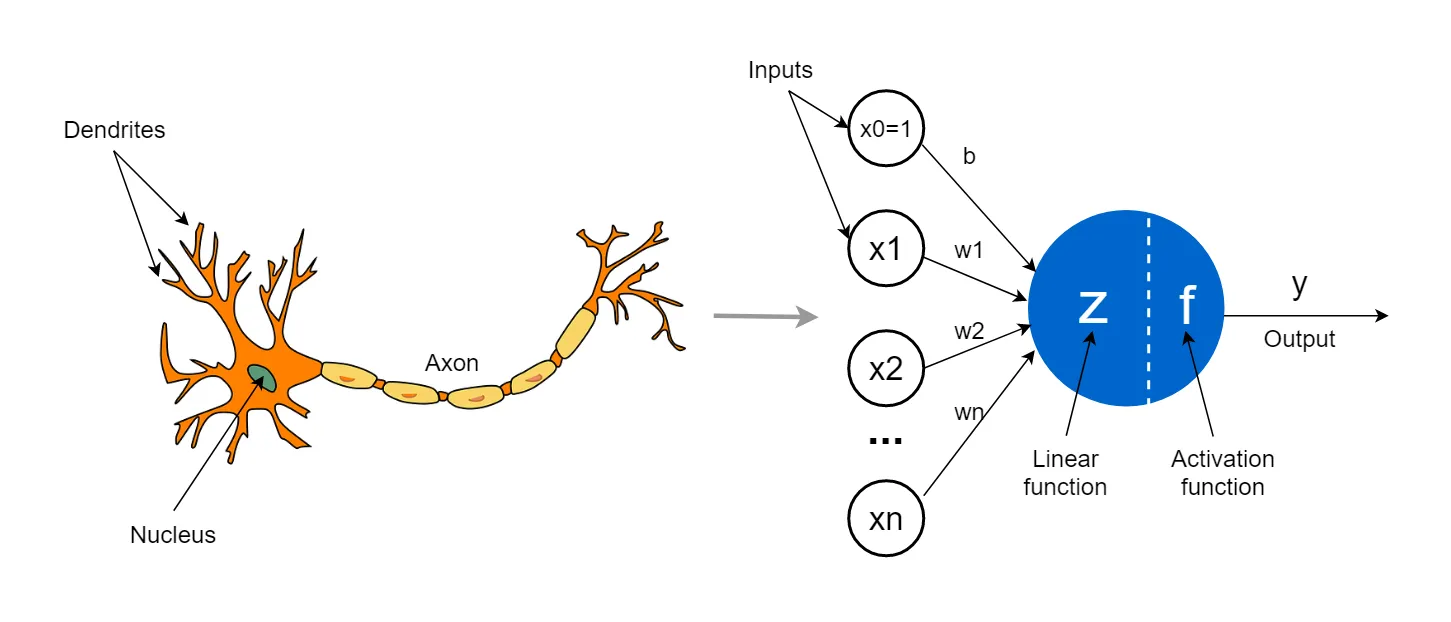
Ta thấy một nơ ron nhân tạo cũng sẽ có ba thành phần là input, trung tâm nơ ron và output, các input \(x_1, x_2, \dots, x_n\) đóng vai trò như dữ liệu đầu vào, các trọng số \(w_1, w_2, \dots, w_n\) đóng vai trò như các tín hiệu ở Dendrites, phần thân nơ ron bao gồm các phép toán và hàm kích hoạt, phần output \(y\) đóng vai trò như Axon.

Nhìn vào hình trên ta có thể thấy nó giống với mô hình thuật toán logistic regression mình đã trình bày ở bài trước, logistic regression chính là một mạng nơ ron nhân tạo có một đơn vị nơ ron. Bây giở ta sẽ đi tìm hiểu một mạng nơ ron nhân tạo đầy đủ sẽ có những thành phần gì:

Nguồn

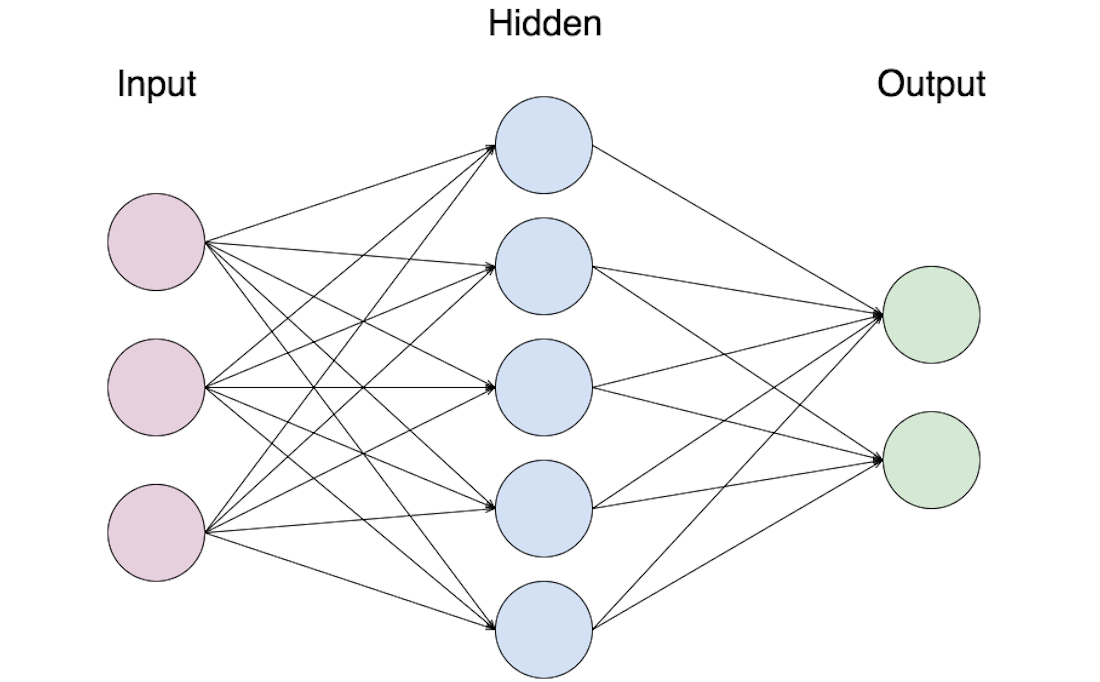
Hình trên là mô hình kiến trúc của một mạng nơ ron đầy đủ sẽ gồm ba lớp: Lớp input (Input layer), lớp ẩn (Hidden layer) và lớp output (Output layer). Lớp input sẽ tiếp nhận thông tin đầu vào, các lớp ẩn sẽ thực hiện quá trình tính toán và quá trình tính toán này sẽ không hiển thị trong quá trình ta training mô hình nói dễ hiểu thì ta không thể biết bên trong các hidden layer đang xảy ra như nào vì thế ta gọi đây là lớp ẩn và lớp ouput để cho ra kết quả cuối cùng của quá trình tính toán.

Một mạng nơ ron sẽ có một lớp Input, một lớp Output và có thể có một hoặc nhiều lớp ẩn ở hình trên là ta đang có một lớp ẩn. Trong nhiều tài liệu ví dụ khi nói mạng nơ ron có 5 lớp thì ta sẽ hiểu người ta đang nói mạng đó có bốn lớp ẩn và một lớp Output, thông thường lớp Input sẽ gọi là lớp 0. Ta có thể thấy mạng nơ ron từ rất nhiều nơ ron kết hợp lại, mỗi nơ ron ở các lớp khác nhau sẽ có nhiệm vụ khác nhau.

Các nơ ron trong mạng nơ ron sẽ được kết nối với nhau, mỗi kết nối sẽ được đặc trưng bởi một trọng số \(w_i\), dạng kết nối thì có thể là đầy đủ hoặc không đầy đủ tùy vào từng bài toán và người thiết kế mô hình, và đầu ra của lớp này chính là đầu vào của lớp kế tiếp.

Ứng dụng

Ứng dụng của neural network ngày nay rất rộng rãi như trong các bài toán về phân loại hình ảnh, xử lí ngôn ngữ tự nhiên…

2. Thiết lập bài toán phân loại ảnh với thuật toán neural network

Bài trước ta đã tìm hiểu về thuật logistic regression từ cách xây dựng hàm mất mát, cách cập nhật bộ trọng số \(\mathbf{w}\) cho đến việc thử áp dụng trong một bài toán phân loại ảnh chó mèo, chúng ta có thể thấy kết quả phân loại chưa được cao, có nhiều lí do dẫn đến hiện tượng này nhưng hiện tại chúng ta chưa bàn đến và ở bài này mình sẽ giữ nguyên bộ data ở bài trước và thực hiện training với thuật toán neural network để chúng ta so sánh được kết quả giữa hai thuật toán này.

Ý tưởng để xây dựng bài toán với thuật thoán neural network nói chung và các bài toán phân loại ảnh nói riêng đều dựa trên các tính năng của input chúng ta gọi là các \(x_i\) (trong bài viết này thì chúng ta định nghĩa các điểm ảnh chính là các \(x_i\)), các tính năng này đi qua mô hình và cho ra output, việc định nghĩa output như thế nào thì trong các  bài toán cụ thể người xây dựng mô hình sẽ định nghĩa, trong bài toán phân loại cats-dogs này thì output được định nghĩa là nhãn của hình ảnh (là cat hoặc dog). 

3. Xây dưng model

Tương tự như bài toán logistic regression ta sẽ có một bộ trọng số \(\mathbf{W}\) và hai nhãn, nhãn 0 là non-cat và nhãn 1 là cat việc học của mô hình chính là việc điều chỉnh bộ trọng số \(\mathbf{W}\) sao cho dự đoán đầu ra theo đúng ý muốn của ta, chỉ khác là đối với logistic regression thì bộ trọng số \(\mathbf{w}\) là một vector vì model chỉ có một nốt tính toán nhưng đối với thuật toán neural network thì mô hình sẽ có nhiều hơn một nốt tính toán nên lúc này bộ trọng số \(\mathbf{w}\) sẽ là một ma trận và sẽ kí hiệu là chữ w in đậm viết hoa: \(\mathbf{W}\). 

Chú ý về ký hiệu: xuyên suốt từ bài này mình sẽ kí hiệu dấu ngoặc tròn \((i)\) để thể hiện điểm dữ liệu thứ \(i\), dấu ngoặc vuông \([l]\) để thể hiện lớp thứ \(l\), và dấu chỉ số \(j\) để hiện nơ ron thứ \(j\), ví dụ \(\mathbf{z}^{[l](i)}_j\) chúng sẽ hiểu là giá trị \(\mathbf{z}\) của nơ ron thứ \(j\) thuộc lớp thứ \(l\) của điểm dữ liệu \(i\).

3.1 Kí hiệu

• Xét trên toàn bộ bộ dữ liệu( m điểm dữ liệu) ta sẽ có một vector hàng \(\mathbf{X} = [\mathbf{x}^{(1)}, \mathbf{x}^{(2)}, \dots, \mathbf{x}^{(m)}]\) với mỗi cột là một điểm dữ liệu \(\mathbf{x}^{i}\) ngăn cách nhau bởi dấu “,”:

\[
\mathbf{X} =
[\mathbf{x}^{(1)}, \mathbf{x}^{(2)}, \dots, \mathbf{x}^{(m)}] =
\left[
\begin{matrix}
x_1^{(1)} & x_1^{(2)} & \dots & x_1^{(m)}\\
x_2^{(1)} & x_2^{(2)} & \dots & x_2^{(m)}\\
\vdots & \vdots & \ddots & \vdots & \\
x_n^{(1)} & x_n^{(2)} & \dots & x_n^{(m)}\\
\end{matrix}
\right]
\]
Ta có thể thấy \(\mathbf{X}\) có được bằng cách xếp thành cột các các \(\mathbf{x}^{(i)}\).

• Mỗi nốt (nơ ron) ở này sẽ được liên kết với tất cả các nốt (nơ ron) bằng các trọng số \(w_i\) do đó bộ trọng số của mỗi nốt (nơ ron)  sẽ là \(\mathbf{w} = [w_1, w_2, \dots, w_n]\) sẽ là một vector hàng, ta sẽ ngăn cách các trọng số \(w_i\)  bằng dấu “,”, trong một lớp sẽ có nhiều nốt (nơ ron) nên sẽ có nhiều bộ trọng số \(\mathbf{w}\), ta sẽ kí hiệu \(\mathbf{w}^{[l]}_j\) là bộ trọng số của nơ ron thứ \(j\) thuộc lớp \(l\), như vậy bộ trọng số của lớp \(l\) sẽ là một ma trận cột với mỗi mỗi hàng là một \(\mathbf{w}^{[l]}_j\) (là ma trận cột là do chúng ta quy ước như vậy).

\[
\mathbf{w}^{[l]}_j = [w_1, w_2, \dots, w_{n^{[l-1]}}]
\]

\[
\mathbf{W}^{[l]} = \left[
\begin{matrix}
\mathbf{w}^{[l]}_1\\
\mathbf{w}^{[l]}_2\\
\vdots\\
\mathbf{w}^{[l]}_{n^{[l]}}
\end{matrix}
\right]
\]

Nếu mô hình có \(L\) lớp thì chúng ta sẽ có \(L\) ma trận \(\mathbf{W}^{[l]}\) 

• Xét trên toàn bộ bộ dữ liệu ta có \(\mathbf{Z}^{[l]} = \mathbf{W}^{[l]}\mathbf{X} + b^{[l]}\) với \(\mathbf{z}^{[l](i)} \) là một vector cột và \(\mathbf{Z^{[l]}}\) là một ma trận hàng:

\[
\mathbf{z}^{[l](i)} = \left[
\begin{matrix}
z^{[l](i)}_1 \\
z^{[l](i)}_2 \\
\vdots \\
z^{[l](i)}_{n^{[l]}}
\end{matrix}
\right]
\]

\[
\mathbf{Z}^{[l]} = \left[ \mathbf{z}^{[l](1)}, \mathbf{z}^{[l](2)}, \dots, \mathbf{z}^{[l](m)}\right]
\]

Tương tự như vậy ta cũng có:

\[
\mathbf{A}^{[l]} = \left[ \mathbf{a}^{[l](1)}, \mathbf{a}^{[l](2)}, \dots, \mathbf{a}^{[l](m)}\right]
\]

3.2 Activate function

Trong mạng neural network thì hàm kích hoạt cho các lớp ẩn thường được sử dụng là Relu function, lí do sử dụng hàm này là vì hàm này thường hiệu quả hơn hội tụ nhanh hơn hàm sigmoid, ngoài relu thì cũng có một số hàm hay được sử dụng nữa là  hàm Tanh , Leaky relu… Trong bài viết này mình sẽ sử dụng hàm kích hoạt cho các lớp ẩn là hàm Relu và hàm để chuẩn hóa đầu ra là hàm sigmoid mặc dù hàm chuẩn hóa đầu ra thường dùng cho neural network là softmax nhưng vì trong ví dụ này chúng ta đang chỉ có hai nhãn nên vẫn sẽ dùng hàm sigmoid để mọi người có thể dễ hiểu hơn vì mình cũng đã sử dụng hàm sigmoid cho bài trước, đối với bài toán nhiều hơn hai nhãn thì sẽ sử dụng hàm softmax cho lớp Output.

Relu function

• Phương trình: 

\[
\begin{align}
\begin{cases}
f(x) = 0 & \text{if } x  < 0 \\
f(x) = x & \text{if } x \geq 0
\end{cases}
\end{align}
\]

hay

\[
f(x) = \max{(0,x)}
\]

• Đồ thị:

Nguồn

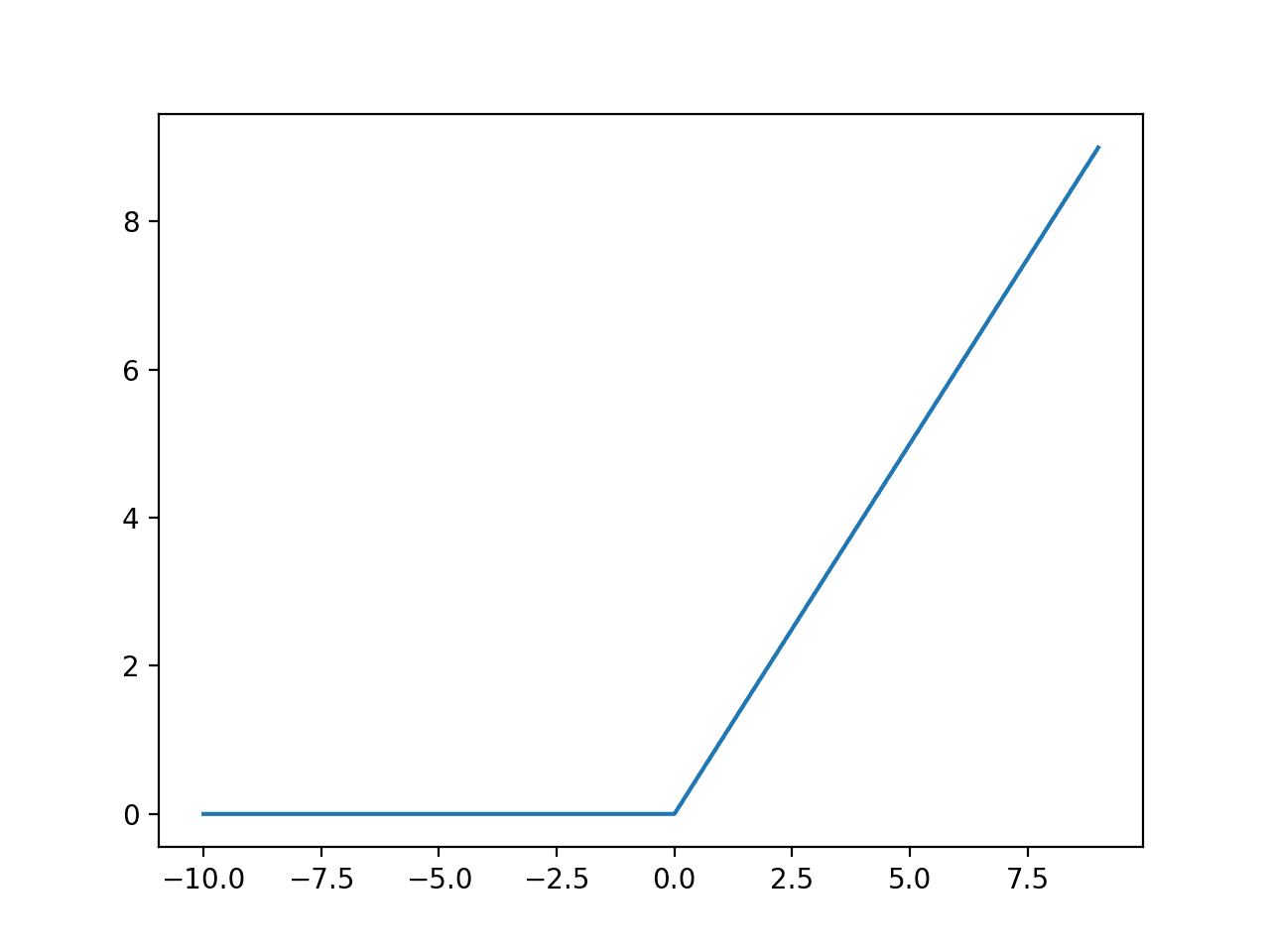
• Đạo hàm:

Ta dễ dàng tính được:

\[
\frac{\partial ReLU(x)}{\partial x} =
\begin{cases}
0 & \text{if } x < 0 \\
1 & \text{if } x > 0 \\
\end{cases}
\]

Ta thấy với \(x = 0\) thì đạo hàm của \(\text{Relu}(x) \) theo \(x\) sẽ không xác định như vậy khi lập trình với giá trị \(x = 0\) ta sẽ mặc nhiên quy ước  \(\frac{\partial ReLU(x)}{\partial x} = 0\).

Sigmoid function

Ở bài trước mình đã trình bày về hàm này nên ở bài viết này mình chỉ nhắc lại.

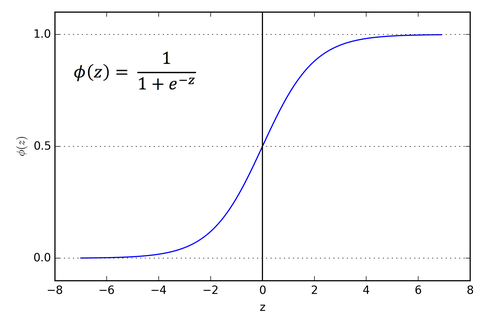
• Phương trình:

\[
\sigma(x) = \frac{1}{1+e^{-x}}
\]

• Đồ thị:

Nguồn

 

• Đạo hàm:

\[
\frac{\partial{\sigma(x)}}{\partial{x}} = (\sigma(x))(1 – \sigma(x))
\]

3.3 model

Ở bài viết lần này mình sẽ xây dựng mô hình gồm một lớp Input, một lớp ẩn và một lớp Ouput, số nơ ron của lớp ẩn sẽ là \(n = 3\), việc chọn mô hình như vậy là để cho dễ hiểu và việc mô phỏng lại quá trình tính toán không quá dài, mục đích không phải là để tạo ra được mô hình dự đoán có độ chính xác cao mà việc chọn mô hình như vậy là mình muốn đơn giản hóa mô hình nhất có thể để mô phỏng lại quá trình tính toán từ đầu đến cuối. Ở hình dưới thể hiện việc tính toán trong mô hình, đây còn được gọi là quá trình foward propagation, chúng ta sẽ làm rõ quá trình này trong mục 3.5.

3.4 Loss function

Loss function cho thuật toán neural network thì ta vẫn sẽ sử dụng hàm có tên là Cross-Entropy:
\[
\mathcal{L}(\mathbf{W}) = -\frac{1}{m}\sum_{i=1}^m(y^{(i)}\log{a^{(i)}} + (1 – y^{(i)})\log{(1 – a^{(i)}}))
\]

Ta có thể biểu diễn hàm mất mát này dưới dạng ma trận:

\[
\mathcal{L}(\mathbf{W}) = -\frac{1}{m}\left(\mathbf{Y}\odot\log{\mathbf{A}} + (1-\mathbf{Y})\odot\log{(1-\mathbf{A})}\right)
\]

Lưu ý là ở cách biểu diễn dạng ma trận hàm loss ta đang thiếu dấu \(\sum\) nếu khi lập trình ta phải viết như này thì với biểu diễn đúng:

\[
\mathcal{L}(\mathbf{W}) = -\frac{1}{m}numpy.sum\left(\mathbf{Y}\odot\log{\mathbf{A}} + (1-\mathbf{Y})\odot\log{(1-\mathbf{A})}\right)
\]

Chú ý: Phép \(\odot\) là phép nhân phần tử (element-wise) không phải nhân ma trận (multiplication matrix).

Nếu chưa hiểu rõ các bạn có thể đọc lại mục loss function ở bài trước.

3.5 Foward propagation

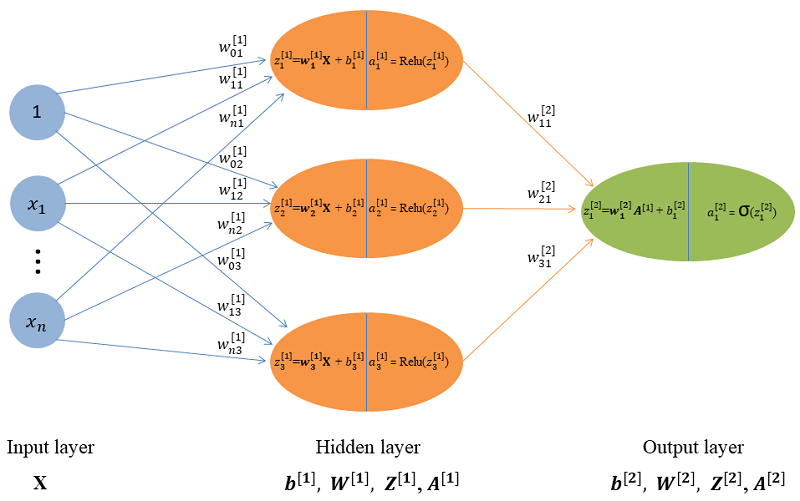
Foward propagation là quá trình tính toán từ Input X => Model => Output, ta có thể thấy ở hình trên từ dữ liệu đầu vào đi qua lớp ẩn và cho ra kết quả ở lớp Output. Giờ ta sẽ đi tính “Foward propagation” từng lớp một mỗi lớp đều sẽ có Input và Output.

Hidden layer:

Ở đây Hidden layer ta chỉ có một lớp 

• Input: \(\mathbf{X} \)
• Output:
  \[
  \mathbf{Z}^{[1]} = \mathbf{W}^{[1]}\mathbf{X} + \mathbf{b}^{[1]} \\
  \mathbf{A}^{[1]} = ReLU(\mathbf{Z}^{[1]})
  \]

Output layer:

• Input: \(\mathbf{A}^{[1]}\)
• Output:
  \[
  \mathbf{Z}^{[2]} = \mathbf{W}^{[2]}\mathbf{A}^{[1]} + \mathbf{b}^{[2]} \\
  \mathbf{A}^{[2]} = \sigma(\mathbf{Z}^{[2]})
  \]

3.6 Backpropagation

Back propagation là quá trình ta đi tìm đạo hàm của các biến theo hàm loss để tìm ra được giá trị mới của các biến đó, ta sẽ đi từ Output layer về Input layer. Để tính được đạo hàm của các biến ta phải nhớ được quy tắc chuỗi:

\[
\frac{\partial{y}}{\partial{x}} = \frac{\partial{y}}{\partial{z}}\frac{\partial{z}}{\partial{x}}
\]
Output layer:

• Tính \(d(\mathbf{A}^{[2]})\):

\[
d(\mathbf{A}^{[2]})
= \frac{\partial{\mathcal{L}}}{\partial{\mathbf{A}}^{[2]}}
= \frac{\mathbf{A}^{[2]} – \mathbf{Y}}{\mathbf{A}^{[2]}(1-\mathbf{A}^{[2]})}
\]

• Tính \(d(\mathbf{Z}^{[2]})\):

\[
d(\mathbf{Z}^{[2]})
= \frac{\partial{\mathcal{L}}}{\partial{\mathbf{Z}}^{[2]}}
= \frac{\partial{\mathcal{L}}}{\partial{\mathbf{A}}^{[2]}}\frac{\partial{\mathcal{A}^{[2]}}}{\partial{\mathbf{Z}}^{[2]}}
= \frac{\mathbf{A}^{[2]} – \mathbf{Y}}{\mathbf{A}^{[2]}(1-\mathbf{A}^{[2]})}\mathbf{A}^{[2]}(1-\mathbf{A}^{[2]})
= \mathbf{A}^{[2]} – \mathbf{Y}
\]

• Tính \(d(\mathbf{W}^{[2]})\):
  

\[
d(\mathbf{W}^{[2]})
= \frac{\partial{\mathcal{L}}}{\partial{\mathbf{W}}^{[2]}}
= \left(\frac{\partial{\mathcal{L}}}{\partial{\mathbf{A}}^{[2]}}\frac{\partial{\mathbf{A}^{[2]}}}{\partial{\mathbf{Z}}^{[2]}}\right)\frac{\partial{\mathbf{Z}^{[2]}}}{\partial{\mathbf{W}}^{[2]}}
= \frac{1}{m}d(\mathbf{Z}^{[2]})\frac{\partial{\mathbf{Z}^{[2]}}}{\partial{\mathbf{W}}^{[2]}}
= \frac{1}{m}d(\mathbf{Z}^{[2]})(\mathbf{A}^{[1]})^T
\]

 

• Tính \(d(\mathbf{b}^{[2]})\):

\[
d(\mathbf{b}^{[2]})
= \frac{\partial{\mathcal{L}}}{\partial{\mathbf{b}}^{[2]}}
= \left( \frac{\partial{\mathcal{L}}}{\partial{\mathbf{A}}^{[2]}}\frac{\partial{\mathbf{A}^{[2]}}}{\partial{\mathbf{Z}}^{[2]}} \right) \frac{\partial{\mathbf{Z}^{[2]}}}{\partial{\mathbf{b}}^{[2]}}
= \frac{1}{m}d(\mathbf{Z}^{[2]}).1
= \frac{1}{m}d(\mathbf{Z}^{[2]})
\]

Lưu ý là hàm loss của ta hiện tại đang biểu diễn theo ma trận nên sẽ bị thiếu dấu \(\sum\) nên khi lập trình \(d(\mathbf{b}^{[2]})\) sẽ được biểu diễn như sau với đúng:

\[
d(\mathbf{b}^{[2]}) = \frac{1}{m}np.sum(d(\mathbf{Z}^{[2]}), axis = 1, keepdims = True) \text{(Tính tổng theo hàng)}
\]

Hidden layer:

• Tính \(d(\mathbf{A}^{[1]})\):

\[
d(\mathbf{A}^{[1]})
= \left(\frac{\partial{\mathcal{L}}}{\partial{\mathbf{A}}^{[2]}}\frac{\partial{\mathbf{A}^{[2]}}}{\partial{\mathbf{Z}}^{[2]}}\right)\frac{\partial{\mathbf{Z}^{[2]}}}{\partial{\mathbf{A}}^{[1]}}
= d(\mathbf{Z}^{[2]})(\mathbf{W}^{[2]})^T
\]

• Tính \(d(\mathbf{Z}^{[1]})\):

\[
d(\mathbf{Z}^{[1]})
= \left(\frac{\partial{\mathbf{L}}}{\partial{\mathbf{A}}^{[2]}}\frac{\partial{\mathbf{A}^{[2]}}}{\partial{\mathbf{Z}}^{[2]}}\frac{\partial{\mathbf{Z}^{[2]}}}{\partial{\mathbf{A}}^{[1]}}\right)\frac{\partial{\mathbf{A}^{[1]}}}{\partial{\mathbf{Z}}^{[1]}}
= d(\mathbf{A}^{[1]})
\]

• Tính \(d(\mathbf{W}^{[1]})\):

\[
d(\mathbf{W}^{[1]})
= \left(\frac{\partial{\mathcal{L}}}{\partial{\mathbf{A}}^{[2]}}\frac{\partial{\mathbf{A}^{[2]}}}{\partial{\mathbf{Z}}^{[2]}}\frac{\partial{\mathbf{Z}^{[2]}}}{\partial{\mathbf{A}}^{[1]}}\frac{\partial{\mathbf{A}^{[1]}}}{\partial{\mathbf{Z}}^{[1]}}\right)\frac{\partial{\mathbf{Z}^{[1]}}}{\partial{\mathbf{W}}^{[1]}}
=\frac{1}{m} d(\mathbf{Z}^{[1]})\frac{\partial{\mathbf{Z}^{[1]}}}{\partial{\mathbf{W}}^{[1]}}
=\frac{1}{m}d(\mathbf{Z}^{[1]})(\mathbf{X})^T
\]

• Tính \(d(\mathbf{b}^{[1]})\):

\[
d(\mathbf{b}^{[1]})
= \left(\frac{\partial{\mathcal{L}}}{\partial{\mathbf{A}}^{[2]}}\frac{\partial{\mathbf{A}^{[2]}}}{\partial{\mathbf{Z}}^{[2]}}\frac{\partial{\mathbf{Z}^{[2]}}}{\partial{\mathbf{A}}^{[1]}}\frac{\partial{\mathbf{A}^{[1]}}}{\partial{\mathbf{Z}}^{[1]}}\right)\frac{\partial{\mathbf{Z}^{[1]}}}{\partial{\mathbf{W}}^{[1]}}
=\frac{1}{m}d(\mathbf{Z}^{[1]})\frac{\partial{\mathbf{Z}^{[1]}}}{\partial{\mathbf{b}}^{[1]}}
=\frac{1}{m}d(\mathbf{Z}^{[1]})1
=\frac{1}{m}d(\mathbf{Z}^{[1]})
\]

Lưu ý là hàm loss của ta hiện tại đang biểu diễn theo ma trận nên sẽ bị thiếu dấu \(\sum\) nên khi lập trình \(d(\mathbf{b}^{[1]})\) sẽ được biểu diễn như sau với đúng:

\[
d(\mathbf{b}^{[1]}) = \frac{1}{m}np.sum(d(\mathbf{Z}^{[1]}), axis = 1, keepdims = True) \text{(Tính tổng theo hàng)}
\]

3.7 Cập nhật trọng số

Sau mỗi một epoch ta sẽ cập nhật giá trị của các \(\mathbf{W}^{[l]}\) và \(\mathbf{b}^{[l]}\) một lần:

\[
\mathbf{W}^{[l]} = \mathbf{W}^{[l]} – \text{learning_rate}*d(\mathbf{W}^{[l]})\\
\mathbf{b}^{[l]} = \mathbf{b}^{[l]} – \text{learning_rate}*d(\mathbf{b}^{[l]})
\]
\(d(\mathbf{W}^{[l]})\) và \(d(\mathbf{b}^{[l]})\) mình đã tính ở phần trên.

4. Xây dựng thuật toán với code python

Ở phần này mình sẽ đi xây dựng và giải thích một số hàm chính, còn lại các hàm khác các bạn có thể tham khảo source code.

Trước khi đi vào phần chính mình có một vài lưu ý:

• Phần code mình viết chỉ đảm bảo là mô tả lại thuật toán, code mình chưa bắt exception nên muốn chạy đúng phải đảm bảo đúng định dạng input.
• Phải đảm bảo data bạn sử dụng đã resize về đúng kích thước. ví dụ bạn để image_widght x image_height là \(128 * 128\) thì bạn phải đảm bảo dữ liệu của bạn đã đúng định dạng \(128 * 128\).
• Config mình sẽ cấu hình trong file config.json
• Nhãn dữ liệu là file label.json
• Link github: https://github.com/trongnghia05/Deep-learning/tree/master/Neural%20network

4.1 Xây dựng hàm khởi tạo init_parameter()

"""
@author Trong Nghia
"""

import numpy as np

def init_parameters(arr_layer):
    L = len(arr_layer)
    parameters = {}

    print("number of layers: " + str(L))
    print("number of layers with parameters: " + str(L - 1))

    for i in range(1, L):
        w = np.random.randn(arr_layer[i], arr_layer[i - 1]) * 0.01
        b = np.zeros((arr_layer[i], 1))

        parameters["W" + str(i)] = w
        parameters["b" + str(i)] = b

    return parameters

 

Input: sẽ là một array_layer chứ số nơ ron các lớp và số lượng lớp ví dụ \([49152‬, 3, 1]\) thể hiện là sẽ có 3 lớp trong đấy lớp đầu tiên là Input, thứ hai là một lớp ẩn, và một lớp Output, số tính năng(có thể coi là số nơ ron) của lớp Input sẽ là \(49152‬ (128*128*3)\) số nơ của lớp ẩn sẽ là \(3\) và số nơ ron của lớp Output là \(1\).

Ta sẽ có một vòng for để khởi tạo trọng số cho từng lớp, ở mỗi vòng lặp ta sẽ có hai tham số cần khởi tạo là giá trị trọng số \(\mathbf{W}\) và giá trị bias \(\mathbf{b}\), đối với giá trị \(\mathbf{W}\) thì ta phải khởi tạo ngẫu nhiên, không thể khởi tạo bằng \(0\) như đối với thuật toán Logistic regression lí do bởi vì nếu ta khởi tạo bằng \(0\) thì giá trị \(\mathbf{W}\) ở các lớp đều như nhau ở các epoch như vậy việc mạng “Deep” sẽ trở nên vô nghĩa, việc chứng minh thì mình sẽ viết trong một bài khác, đối với giá trị \(\mathbf{b}\) thì ta có thể khởi tạo ngẫu nhiên hoặc khởi tạo bằng \(0\), ở đây mình đang khởi tạo giá trị này bằng \(0\).

Output: Output của hàm này sẽ là một array chứa các tham số được khởi tạo ở tất cả các lớp.

4.2 Xây dựng hàm tính toán xuôi foward_propagation()

"""
@author Trong Nghia
"""

import numpy as np

def forward_propagation(X, parameters, activation_param_setting):
    caches = []
    A_prev = X
    L = len(parameters) // 2 + 1

    for i in range(1, L):
        W = parameters["W" + str(i)]
        b = parameters["b" + str(i)]
        Z = np.dot(W, A_prev) + b

        if activation_param_setting[i - 1] == "relu":
            A = relu(Z)
        elif activation_param_setting[i - 1] == "sigmoid":
            A = sigmoid(Z)

        cache = (A_prev, W, b, Z)
        A_prev = A
        caches.append(cache)

    return A, caches

 

Input:

• X là dữ liệu đầu vào có chiều là \((49152‬, m)\) với m là số điểm dữ liệu(số lượng ảnh train), ở đây ảnh đầu vào của mình là \(128*128*3\).
• Parameters là array được khởi tạo ở hàm init_parameter().
• activatie_param_setting là một array chứa dạng kích hoạt của các lớp tính toán, ví dụ [“relu”,”sigmoid”] biểu thị hàm kích hoạt của lớp ẩn thứ nhất là “relu“(ở đây mình chỉ có một lớp ẩn), “sigmoid” là hàm kích hoạt của lớp Output.

Ở đây ta cũng sẽ có một vòng for để tính toán cho từng lớp tức mỗi vòng lặp sẽ tính cho một lớp (lưu ý ở đây tuy mô hình ta có 3 lớp nhưng chỉ có 2 lớp tham gia quá trình tính toán là lớp ẩn và lớp Output), các tham số cần tính ở mỗi lớp sẽ là: \(\mathbf{W}^{[l]}\), \(\mathbf{b}^{[l]}\), \(\mathbf{Z}^{[l]}\), \(\mathbf{A}^{[l]}\), “\(l\)” biểu thị tên lớp hiện tại, công thức tính các tham số này mình đã tính ở phần Foward propagation.

Output: Output của hàm này sẽ  là giá trị Output cuối cùng(\(\mathbf{A}^{[2]}\) ở trong code mình kí hiệu giá trị cuối cùng là \(AL\)) và array caches chứa các giá trị \(\mathbf{W}^{[l]}\), \(\mathbf{b}^{[l]}\), \(\mathbf{Z}^{[l]}\), \(\mathbf{A}^{[l]}\) ở các lớp vừa tính được.

4.3 Xây dựng hàm tính toán ngược back_propagation()

"""
@author Trong Nghia
"""

import numpy as np

def back_propagation(AL, Y, caches, activation_param_setting):
    m = Y.shape[1]
    dA = (AL - Y) / (AL * (1 - AL))
    L = len(caches)
    Y = Y.reshape(AL.shape)
    grads = {}

    for i in reversed(range(L)):
        A_prev, W, b, Z = caches[i]

        if activation_param_setting[i] == "sigmoid":
            dZ = sigmoid_backward(dA, Z)
        elif activation_param_setting[i] == "relu":
            dZ = relu_backward(dA, Z)

        dA_prev = np.dot(W.T, dZ)
        dW = np.dot(dZ, A_prev.T) / m
        db = np.sum(dZ, axis=1, keepdims=True) / m

        grads["dA" + str(i)] = dA_prev
        grads["dW" + str(i + 1)] = dW
        grads["db" + str(i + 1)] = db
        grads["dZ" + str(i + 1)] = dZ

        dA = dA_prev

    return grads

 

Input:

• AL: Giá trị Output cuối cùng của mô hình(giá trị dự đoán của mô hình).
• Y: Giá trị thực( giá trị đúng) của các điểm dữ liệu.
• caches: array chứa các tham số của quá trình foward propagation.
• activatie_param_setting: là một array chứa dạng kích hoạt của các lớp tính toán, ví dụ [“relu”,”sigmoid”] biểu thị hàm kích hoạt của lớp ẩn thứ nhất là “relu“(ở đây mình chỉ có một lớp ẩn), “sigmoid” là hàm kích hoạt của lớp Output.

Ta cũng có một vòng for để lặp qua các lớp, nhưng ở đây mình sẽ lặp ngược từ lớp Output đến lớp Input vì đây là quá trình tính toán ngược phục vụ cho việc cập nhật tham số, mỗi vòng lặp sẽ tính đạo hàm của các giá trị \(\mathbf{W}^{[l]}\), \(\mathbf{b}^{[l]}\), \(\mathbf{Z}^{[l]}\), \(\mathbf{A}^{[l]}\) theo hàm mất mát, ở mỗi vòng lặp mình đều lưu giá trị vào dictionary grads, các công thức tính toán mình đã tính ở phần Backpropagation.

Output: Output của hàm này sẽ là một dictionary chứa các tham số đạo hàm \(d(\mathbf{W}^{[l]})\), \(d(\mathbf{b}^{[l]})\), \(d(\mathbf{Z}^{[l]})\), \(d(\mathbf{A}^{[l]})\).

4.4 Xây dựng hàm cập nhật tham số update_parameter()

"""
@author Trong Nghia
"""

def update_parameters(parameters, grads, learning_rate):
    L = len(parameters) // 2

    for i in range(L):
        parameters["W" + str(i + 1)] -= learning_rate * grads["dW" + str(i + 1)]
        parameters["b" + str(i + 1)] -= learning_rate * grads["db" + str(i + 1)]

    return parameters

 

Input:

• parameters: Array chứa các tham số mô hình là \(\mathbf{W}^{[l]}\) và \(\mathbf{b}^{[l]}\) ở các lớp.
• grads: Dictionary chứa các giá trị đạo hàm của các tham số mô hình theo hàm mất mát ở các lớp.
• learning_rate: Là tốc độ cập nhật tham số( tốc độ học).

Việc cập nhật tham số sẽ được tính theo công thức mà mình đã viết ở phần Cập nhật trọng số.

Output: Output của hàm này sẽ được array parameters đã được cập nhật.

4.5 Xây dựng hàm tính giá trị loss compute_cost()

"""
@author Trong Nghia
"""

import numpy as np

def compute_cost(AL, Y):
    m = Y.shape[1]
    cost = -np.sum((Y * np.log(AL)) + (1 - Y) * np.log(1 - AL)) / m
    cost = np.squeeze(cost)

    return cost

Input của hàm này sẽ là giá trị \(\mathbf{AL}\)(giá trị mô hình dự đoán) và giá trị thực \(\mathbf{Y}\) của các điểm dữ liệu, công thức tính mình đã trình bày ở phần Loss function.

Output của hàm này sẽ là giá trị cost(ở đây mình đang viết là cost thực chất cost là người ta dùng để giá trị mất mát của cả tập dữ liệu còn loss thì để chỉ giá trị mất mát của một điểm dữ liệu).

4.6 Xây dựng hàm đào tạo fit()

"""
@author Trong Nghia
"""

import copy
import numpy as np

def fit(X, Y, parameters, activation_param_setting, epoch, learning_rate):
    costs = []
    model = {}
    arr_epoch = np.arange(1, epoch + 1, 100)

    for i in range(epoch):
        AL, caches = forward_propagation(X, parameters, activation_param_setting)
        cost = compute_cost(AL, Y)
        grads = back_propagation(AL, Y, caches, activation_param_setting)
        parameters = update_parameters(parameters, grads, learning_rate)

        if i % 100 == 0:
            print("cost epoch " + str(i) + ": " + str(cost))

        model[str(i)] = copy.deepcopy(parameters)
        costs.append(cost)

    return costs, arr_epoch, model

 

Input: Giá trị input là các tham số và array mình đã trình bày ở các hàm trên, ở đây có thêm tham số epoch, tham số này là số lần mà ta train mô hình.

Việc tính toán bên trong hàm này chính là gọi đến các hàm phía trên, hàm foward_propagation để tính toán xuôi, sau khi tính xong ta sẽ gọi đến hàm compute_cost để tính giá trị loss, việc tính giá trị này là để ta biết được tình trạng đang học của mô hình thế nào, sau đó ta sẽ đến hàm back_propagation để tính đạo hàm các giá trị theo hàm mất mát, sau đó ta sẽ gọi đến hàm update_parameter để cập nhật lại tham số, ở đây mình đang để cứ mỗi khi lặp được 100 lần thì mình sẽ lưu lại giá trị của hàm loss và giá trị bộ tham số một lần, việc lưu lại giá trị loss để phục vụ cho việc vẽ biểu đồ và lưu lại giá trị bộ tham số để sau này ta có thể chạy thử nghiệm với tập Test với nhiều bộ tham số khác nhau, số lần ta lặp lại quá trình này bằng giá trị của epoch.

Output: Output của hàm này sẽ là hai array costs và arr_epoch để phục vụ cho việc vẽ đồ thị và dictionary model chứa các bộ tham số khác nhau ở các lần lặp để phục vụ cho quá trình thử nghiệm.

4.7 Xây dựng hàm dự đoán predict()

"""
@author Trong Nghia
"""

def predict(X, parameters, activation_param_setting):
    AL, caches = forward_propagation(X, parameters, activation_param_setting)

    label_predict = np.zeros((1, AL.shape[1]))
    num_label_1 = 0
    num_label_0 = 0

    for i in range(AL.shape[1]):
        if AL[0][i] > 0.5:
            label_predict[0][i] = 1
            num_label_1 += 1
        elif AL[0][i] == 0.5:
            label_predict[0][i] = 0.5
        else:
            label_predict[0][i] = 0
            num_label_0 += 1

    return label_predict, num_label_1, num_label_0

 

Input của hàm này giống như hàm fit() nhưng sẽ không có giá trị thực \(\mathbf{Y}\) của các điểm dữ liệu vì ta sẽ không dùng đến ở hàm này, quá trình tính toán của hàm này chỉ khác với hàm fit() là chỉ có quá tính toán xuôi để tính được \(\mathbf{AL}\) (giá trị dự đoán) chứ không có phần tính đạo hàm và cập nhật tham số, threshold (ngưỡng) để phân loại sẽ là \(0.5\).
Output của hàm này sẽ là array label_predict chứa nhãn dự đoán đối với tập test của mô hình mình, number_label_1 là số ảnh là nhãn \(1\), number_label_0 là số ảnh là nhãn \(0\).

4.8 Kết quả

Với epoch là 10000, learning rate là 0.0075 ta được giá trị loss khá thấp, độ chính xác trên tập train là khoảng 98% và trên tập test toàn nhãn 1 là 76 % đã có cải thiện hơn so với thuật toán logistic regression nhưng mô hình sử dụng thuật toán neural network này cũng bị overfitting, có thể thấy ở đây mình đang dể epoch là 10000 nên mọi người có thể thử để thấp hơn để thử nghiệm, miền chung so với thuật toán logistic regression thì neural network đã có cải thiện hơn, để độ chính xác cao trên cả tập train và tập test thì ngoài vấn đề về mô hình thì còn các yếu tố khác như độ lớn của epoch, learning_rate và cả bộ dữ liệu tốt. Dưới đây là giá trị cost qua các vòng lặp, trục ngang là epoch, còn trục dọc là giá trị cost:

Ở bài sau ta sẽ đi tìm hiểu về thuật toán Convolution neural network (CNN) và so sánh với thuật toán neural network thuần, đây là thuật toán hiện nay được dùng phổ biến trong bài toán phân loại.

5. Tài liệu tham khảo

1. https://en.wikipedia.org/wiki/Neuron